Resistors may be used to represent various electrical components used in practice. One such example is a light bulb that behaves like a resistor. It is therefore important to understand how current and voltages vary when resistors are in series or in parallel.
Resistors in Series
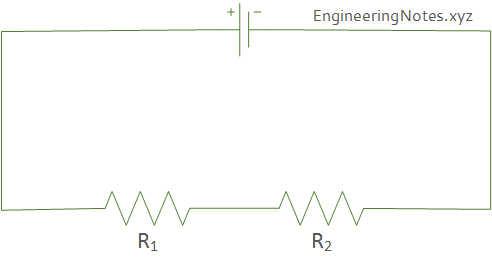
Resistors are combined in series as shown in Figure 1.
Figure 1: Resistors R1 and R2 connected in series
The formula for calculating the effective resistance \(R_{eff}\) is
\(R_{eff} = R_1 + R_2 \)
The above diagram can then be simplified with only one resistor with resistance \(R_{eff}\) instead of two.
For a circuit with more than two resistors in series, the same addition principle applies. Say the circuit has n resistors, effective resistance becomes
\(R_{eff} = R_1 + R_2 + R_3 + \dots + R_n \)
Resistors in Parallel
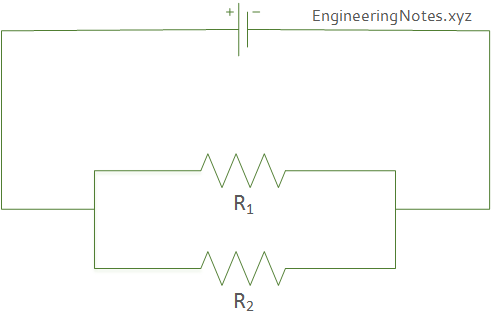
Resistors can also be combined in parallel circuits as shown in Figure 2.
Figure 2: Resistors connected in parallel
The effective resistance \(R_{eff}\) is given by
\(\large{\frac{1}{R_{eff}} = \frac{1}{R_1} + \frac{1}{R_2}}\)
The above equation is can be rewritten as
\(R_{eff} = \frac{R_1 R_2}{R_1 + R_2}\)
In the case of circuits with more than two resistors, the general equation is
\(\large{\frac{1}{R_{eff}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \ldots + \frac{1}{R_n}}\)
Example
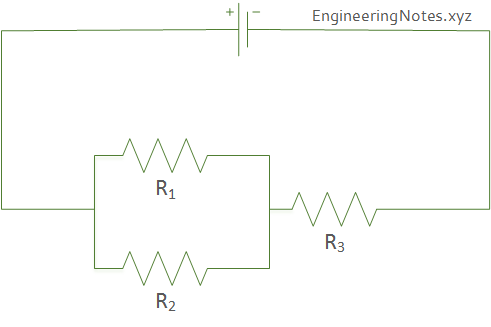
Consider the circuit shown in Figure 3 below.
Figure 3: Circuit with a combination of series and parallel resistors
Resistors \(R_1\) and \(R_2\) are in parallel and can be combined using the above equation
\(R_{1,2} = \frac{R_1 R_2}{R_1 + R_2}\)
Next, the overall effective resistance can be found by combining \(R_{1,2}\) with \(R_3\). Since they are in series, the resistances are added.
\(R_{eff} = R_{1,2} + R_3 \)